The beginner method to solve a 4x4 is called reduction. The concept is that you reduce the cube to a 3x3. There are three big parts to solving a 4x4 cube with this method namely:
- Solve the Centers
- Pair the Edges
- Solve 3x3 Stage (with possible parity)
PART1: Solve the CENTERS
The first part is to solve the six centers. The centers of a 4x4 is not fixed. It is necessary to solve the centers into the correct position relative to each other.
This tutorial will solve the six centers of a 4x4 in the following order:
1. White
2. Yellow (Opposite White)
3. Green (In between White and Yellow)
4. Orange (Next to Green in the front face with Yellow on the left and White on the right)
5. Solve Red (opposite Orange) and Blue (opposite Green) together.
IMPORTANT: This step is generally done intuitively. The concept explained in this 4x4 tutorial is to make a "bar" (2 centers pieces together) and then put the bars together to form a center.
1. Solve the White Center
- Find two white center pieces. In the image below they are on adjacent sides, but sometimes the two pieces may be on opposite sides of the cube.
- Turn the outer layers until the two white centers will come together and form a “bar” when you move the inner layers together. You may need to turn the outer layers 1,2 or 3 times depending on where the white center is located.

- Turn your cube so that the White “bar” is on top. Make the second White bar and put it together with the first.

- If you have a center piece at the bottom then use the steps below to make the second White bar and put it together with the first.

-
If you have 3 center pieces together then use the steps below to put the last center piece in place.

This process is intuitive; you can do it for sure, but it takes a little practice.
2. Solve the Yellow Center opposite White.
- Hold the cube so that the White center is at the bottom.
- Use the 2 inner horizontal layers to make a Yellow “bar” in the front face.
- Turn the front face so that the pair is in the right-hand side.
- Place the Yellow center pair in the top layer without messing up the White center using the following algorithm.

-
Use the middle layer to make the second Yellow “bar”.
-
Turn the top face and front face so that the 2 yellow bars are on the righthand side in the same column. Pair the bars up in the top layer using the following algorithm.

Possible problem: You may have three center pieces together . Perform the steps below to complete the Yellow center.

3. Solve the Green center

- Hold the cube so that the white center is still at the bottom and the yellow center is on top.
- As before you make a Green “bar” using the inner horizontal layers. Do not move the “vertical” inner layers as this will break your yellow and white centers.
- Turn the layer with the Green “bar” so that the bar is horizontal. This way you will not break it when making your second Green “bar”.

-
Turn the outer layers to orientate the 2 white bars correctly so that you can move them next to each other. Be sure not the break the white or yellow centers.

4. Solve the Orange center
Put the completed Green center at the bottom, with the Yellow center on the left and White center on the right. Make an Orange "bar" by moving two Orange pieces together, turning the face so the "bar" is vertical then restore the centers.
Repeat this to make second Orange bar this time with Green in the Back and the already completed Bar in the Bottom.

Then follow the instructions below to put the two orange bars together without messing up the completed centers.

Possible problem: You may have three center pieces together. Perform the steps below to make your Orange Center.

5. Solve the Red and Blue centers.
There are seven cases for solving the last two centers. In the pictures below the Top face should be Blue and the front face Red.



IMPORTANT: Check that your centers are correct.
- White opposite Yellow
- Blue opposite Green
- Red Opposite Orange.
- If White is on top and Blue is facing you, then Red must be on the left and Orange on the Right.
If your centers are not in the correct position then you can use the following algorithms to correct the centers.

PART 2: Pair the Edges
Pair all 12 edges
The second part in solving a 4x4 cube is to pair the edges, which involves matching two edge pieces with the same colors.
On a 4x4, each edge is made up of two pieces, unlike a 3x3 where each edge consists of just one piece. The goal of this step is to pair up the matching edge pieces on all 12 edges, so that each edge behaves like a single edge on a 3x3 cube. Once all the edges are paired, the 4x4 cube is effectively reduced to a 3x3, and you can proceed to solve it just like you would a regular 3x3 cube.

The Concept:

At the beginner level, you will move the edges that you want to pair into the front-left and front-right positions of the cube. This will enable you to make and store the pair, without disturbing the rest of the cube.
The secret of this step is to always bring an unpaired edge back into the front right slot so that solved pieces are not disturbed when you restore your centers after an edge pair.
a) Setup to pair edge
1. Find Two Matching Edges:
Look for two edge pieces that have the same colors. These are the pieces you need to pair together.
2. Move the Matching Edges into Position
Once you've found a matching pair, move the two edge pieces into the front-left and front-right positions of the cube. Do this by turning the outer layers only (the top, front, and side layers).
IMPORTANT: Do not turn any inner layers for this step. This will disrupt the centers you made in part 1.
If the matching edges are on the top layer (but not in the front-left or front-right positions), you'll need to move them into position. You can use the outer layers to adjust their placement without touching the inner layers. Use the steps below as a guide.




b) Pair Edge and Store
The next step is to pair the edge that you setup in the previous step and store the paired edge in the top layer.
IMPORTANT: Make sure that you always have an unpaired edge in the top layer as this will go into the paired edge slot.
This step breaks the centers, but it will be restored once you moved the paired edge into the top layer.
Slice the Top or Bottom Layer:
- Slice (turn) the Top or Bottom half of the cube to move the matching edges together.
1) Pair the edges
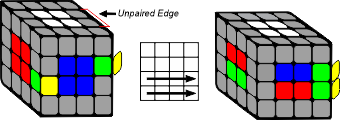
OR

2) Move the Paired Edges to the Top:
- After pairing the edges, move the paired edges to the top layer.
- While doing this, make sure to bring down an unpaired edge to replace the newly paired edge before slicing back to restore the original state.

3) Restore the Center

Top is “FULL”:
Once the top layer has four paired edges then turn the cube around so that you can store paired edges on the other side of the cube. Note: The paired edges are now in the bottom layer.
c) Repeat Edge Pairing for 10 edges

Repeat this process for 10 edges. Each time, make sure that you have an unpaired edge in the top layer, so you can pair it with the corresponding slot
Summary:
- Always keep an unpaired edge in the top layer.
- Slice the top or bottom layer to pair the edges.
- Move the paired edges to the top layer and bring down an unpaired edge before slicing back.
d) Last Edge Pair
For the past edge pair you will have two “unpaired edges” with the same two different pieces. For this step same edges need to be in the same horizontal layer on both sides. You will now perform the middle slice as if you were pairing the edges, then flip the edge and slice back to pair the edges. Note the pair will only be made with the last slice back move.
PART3: Solve using 3x3 method
Now that you have all your centers complete and edges paired you can solve the cube as you would a 3x3.
Possible Problem: Whilst solving the last layer of the 3x3 stage, you may come across a problem where it seems like a last layer edge is flipped, or only two edges are swapped, which is impossible on a 3x3. This is called parity.
The following pages show you how to solve the Parity:





